Conjuntos

CLASE 25 02/07/2019

«El éxito es saber tu propósito en la vida, crecer para alcanzar tu máximo potencial y plantar semillas que beneficien a otros»

John C. Maxwell

Unión de conjuntos

Supongamos que tenemos los conjuntos  M y N definidos como se muestra en la siguiente figura:

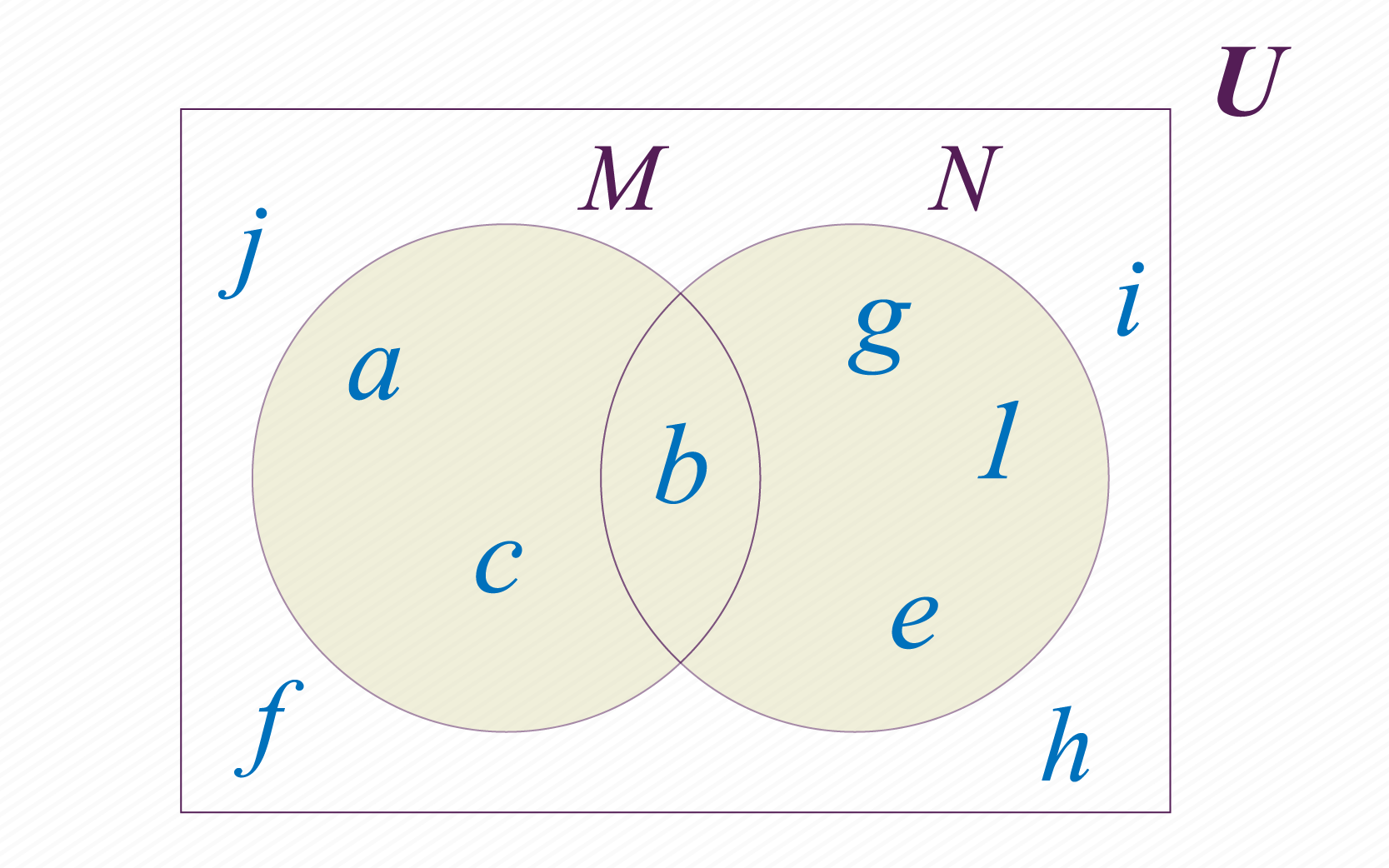
Podemos crear otro conjunto conformado con los elementos que pertenezcan a M  o a N.  A este nuevo conjunto le llamamos unión de  M y N, y lo notamos de la siguiente manera: En la imagen de abajo puedes observar el resultado de unir los conjuntos  M y N .

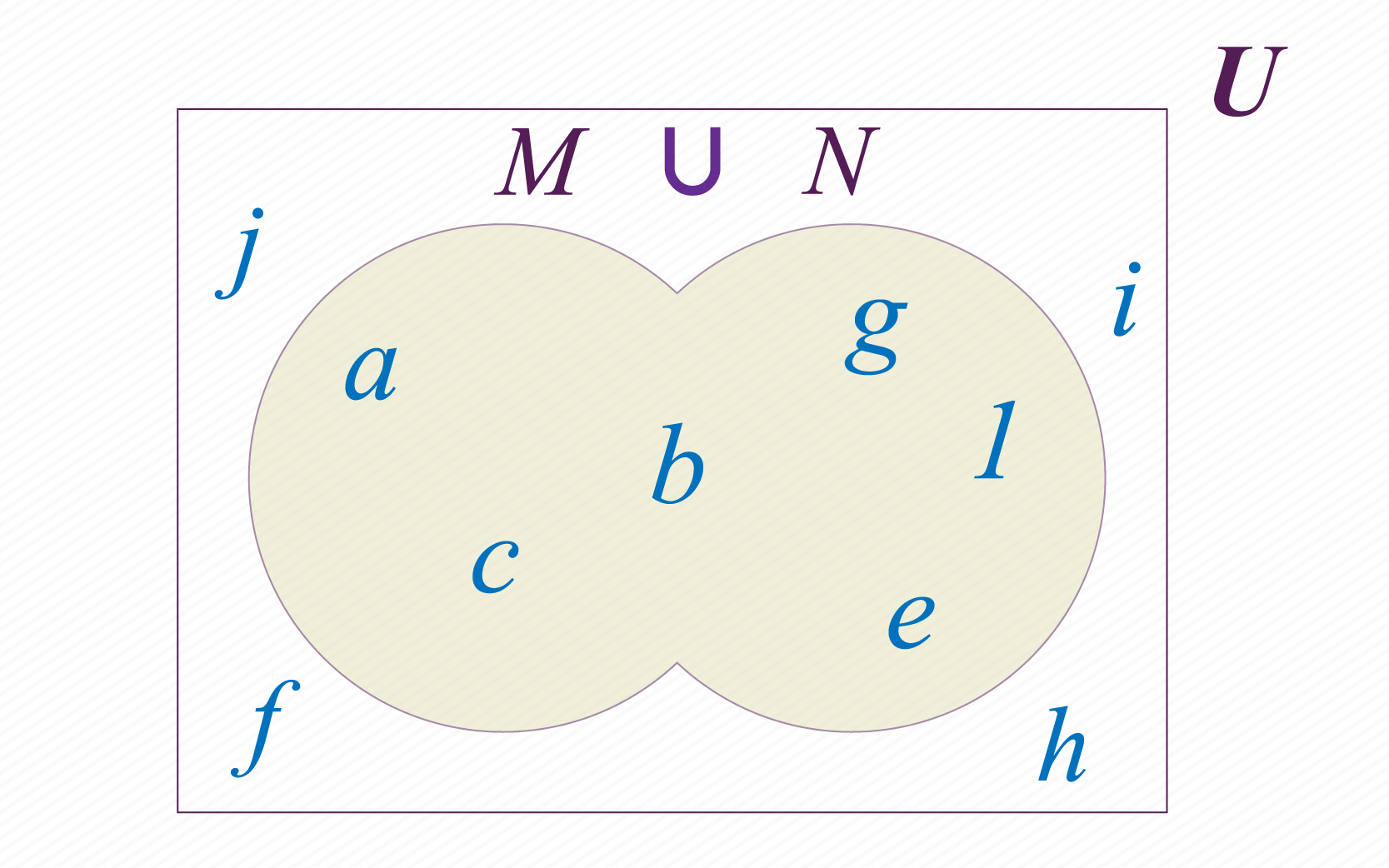
Al elegir qué elementos estarán en la unión de nuestros conjuntos  y , debes preguntarte cuáles están en el conjunto M “o” N en el conjunto .  El resultado de la operación será el conjunto conformado por todos los elementos del conjunto universal , que cumplan la condición de estar en uno o en otro.

Tenemos en este caso: :

Intersección de conjuntos

Sigamos tomando como ejemplo los conjuntos  M y N definidos anteriormente.  Podemos determinar un nuevo conjunto conformado por los elementos que nuestros conjuntos  y  tienen en común.  A este nuevo conjunto le llamamos intersección de  M y N , y lo notamos de la siguiente manera: .

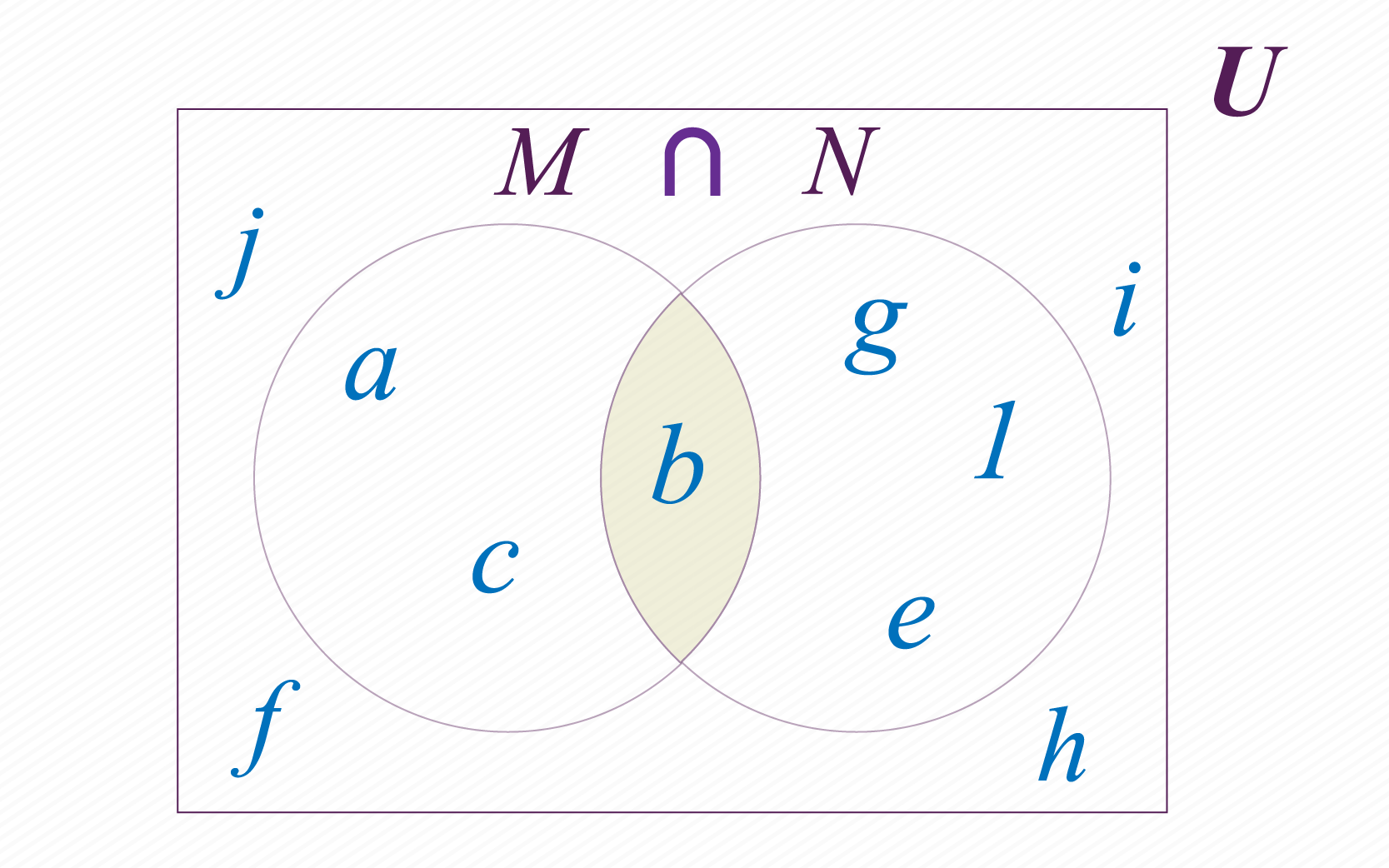
Para determinar que elementos pertenecen a la intersección de los conjuntos  y te puedes preguntar qué elementos están en M “y” N en   Todos los elementos del conjunto  que cumplan esta condición deberán estar en el conjunto .  En la figura de la arriba puedes ver la intersección de nuestros conjuntos  M y N.

Diferencia de conjuntos

Además de la unión y la intersección podemos realizar la diferencia de conjuntos.
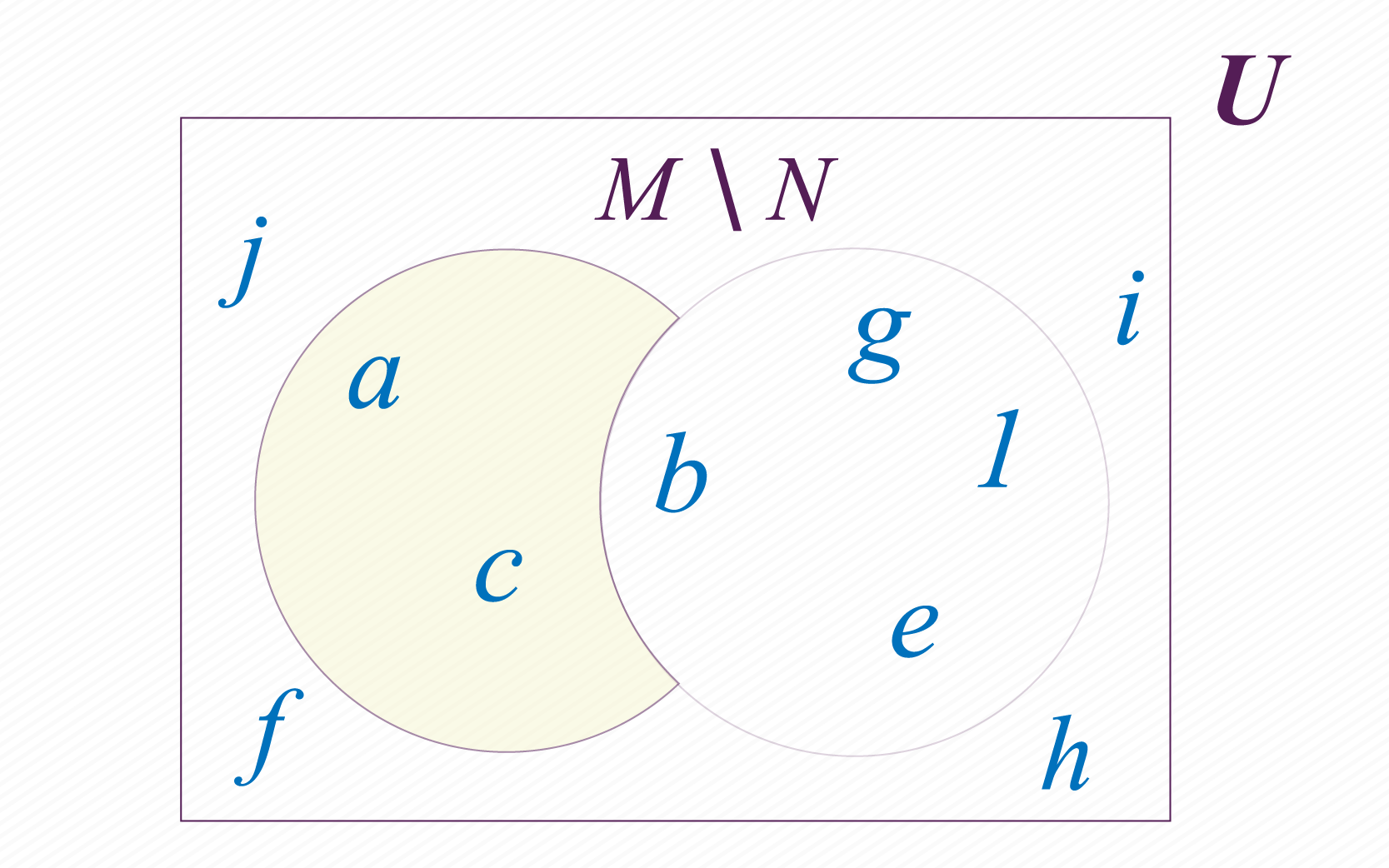
En este caso se deben seleccionar los elementos de un conjunto que no estén en el otro.  Por ejemplo, si realizas la operación M menos N , debes seleccionar los elementos de M que no están en N .  Representamos la diferencia M menos N así: .  Observa que en este caso .

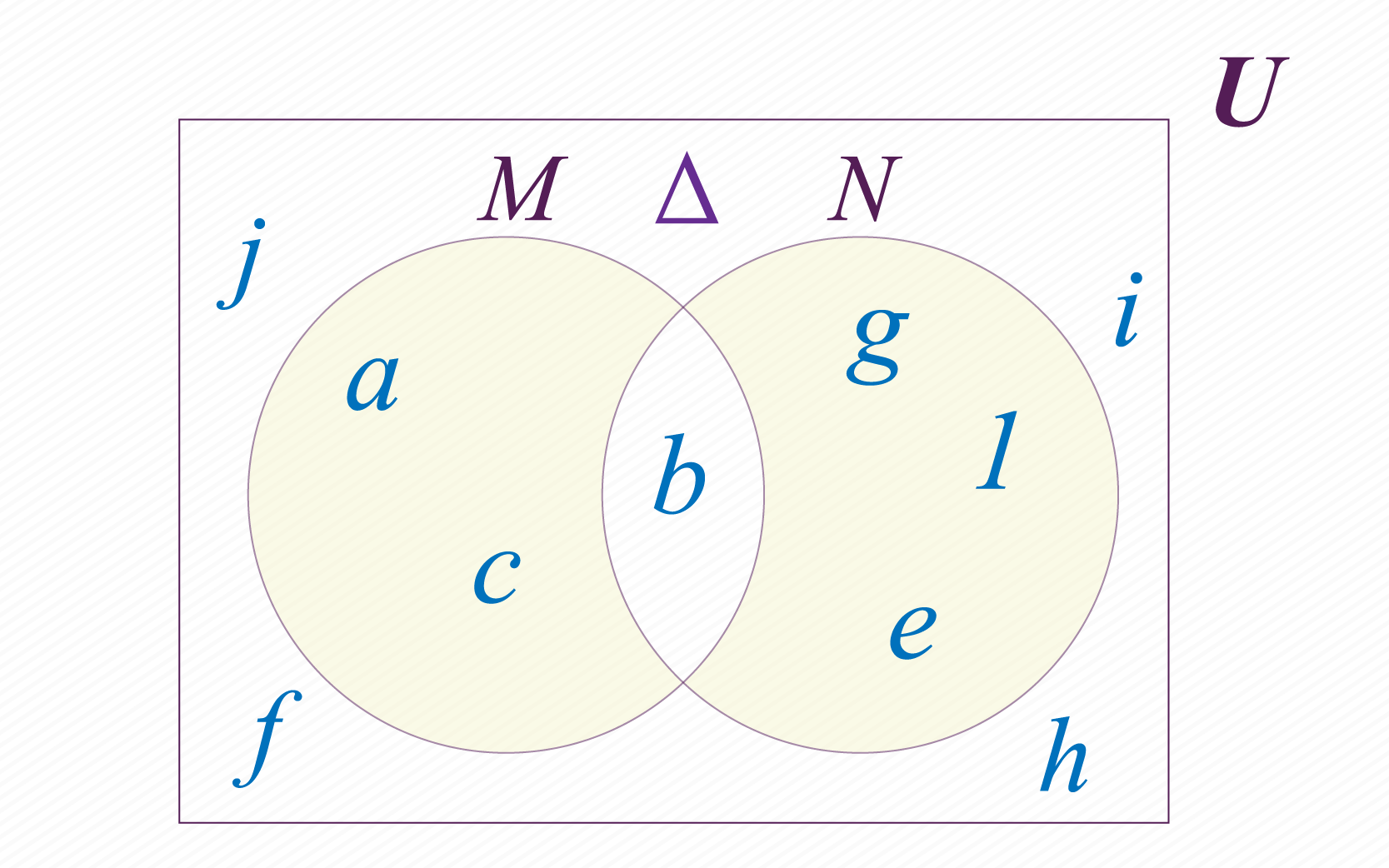
Diferencia simétrica de conjuntos

Que el nombre esta operación no te alarme, también es muy sencilla. En esta ocasión se deben escoger los elementos de M que no están en N , y los elementos de N que no están en M.  Puedes ver el resultado de la diferencia simétrica entre M y N en la figura de abajo.  Representamos la diferencia simétrica a través del símbolo .  En el caso de nuestros conjuntos M y N y tenemos.

Complemento de un conjunto

La ultima operación que estudiaremos no es entre dos conjuntos.  Decimos que el complemento de M es el conjunto conformado por todos los elementos del conjunto universal , que no pertenecen al conjunto M.  Es común usar los símbolos Mc o M´, para representar el complemento del conjunto.

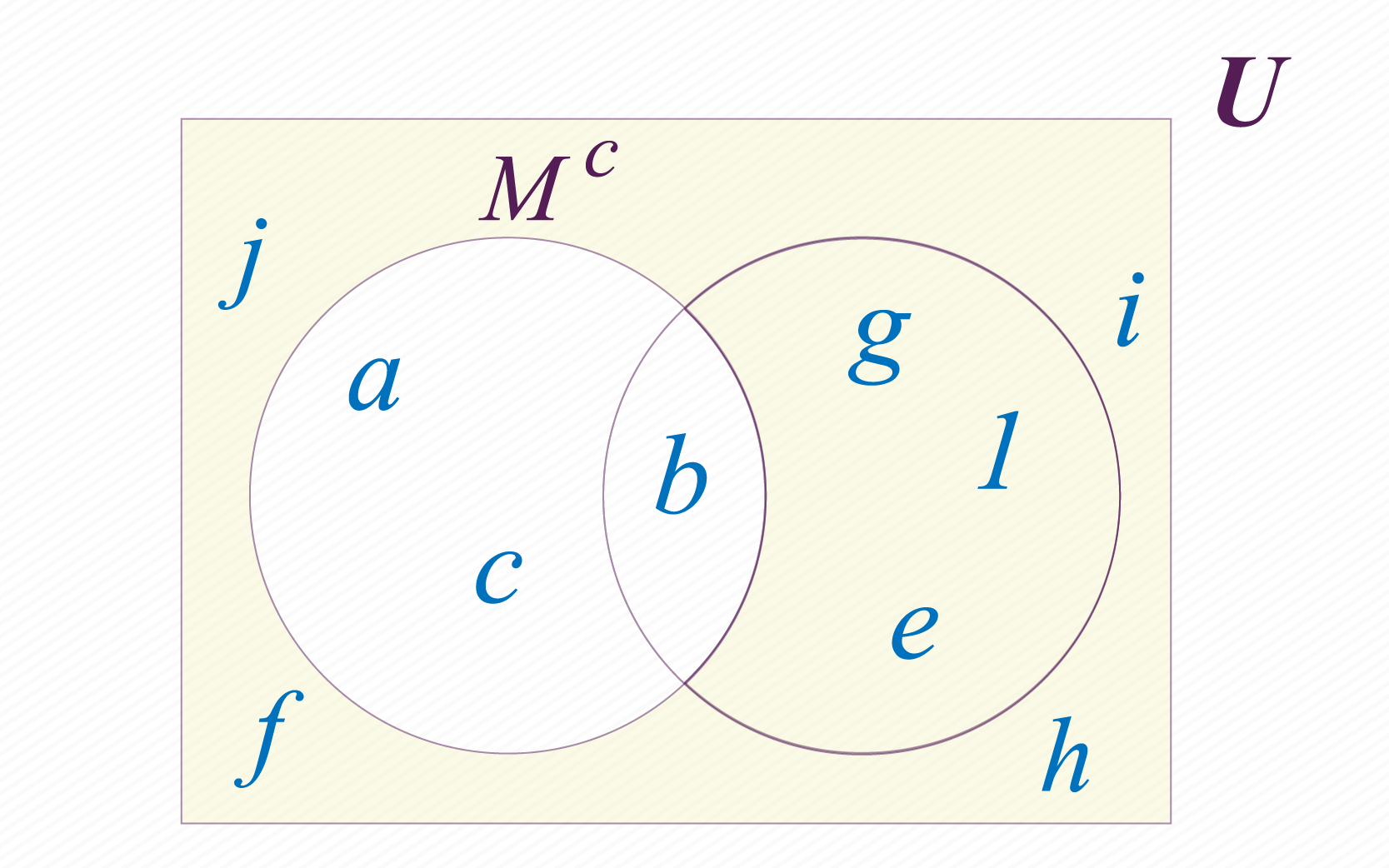
Aprendizajes del día:

-A pesar de ser un tema que hemos visto de años atrás, aún se nos dificulta el hecho de realizar operaciones entre estos pues no sabemos diferenciar bien lo que se debe hacer. -En lo personal no se me hace tan difícil este tema, aunque considero que debo repasar un poco más para comprender mejor y no tener tantas dudas. -La manera en la que lo hemos ido trabajando en el aula ha sido de mucha ayuda pues el licenciado nos resuelve las dudas y si es necesario lo vuelve a repetir. -He comprendido un poco mejor el tema con ayuda de mis compañeras pues han sido ellas quienes me han explicado y me han ayudado a resolver algunos problemas que no sabía como era. -Debo poner mucha atención desde el inicio de la clase pues esto ayudará a comprender todo el tema y no tener que estar interrumpiendo la clase para preguntar algo que no entendí por no prestar atención. Los temas están conectados por lo que todos son sumamente importantes.

Adriana Garzaro